De temps à autre il nous est fait la remarque, ou alors c'est nous qui avons l’occasion de le lire ailleurs, que le fait de disposer de fichiers audio en 192 kHz, donc capables de contenir, d'après le Théorème de Shannon, des signaux jusqu'à 96 kHz, ne présente pas d’intérêt puisque l’audition d’un être humain dans l’aigu n’excède pas, dans les meilleurs des cas, 20 kHz.
Ce dernier point n’est pas faux, mais si les fichiers échantillonnés à 192 kHz, ou même à 96 kHz, ne présentaient aucun autre intérêt que cette augmentation de la fréquence maximale des signaux enregistrables, nous ne manquerions pas de le dire, ce qui ne serait certes pas dans l'intérêt de Qobuz pour la vente de ses fichiers Studio Masters, mais tout simplement de l’honnêteté de notre part...
C'est pour cela que nous allons apporter quelques précisions que nous pensons bien utiles, pour ne pas dire nécessaires, sur "l'échantillonnage", en commençant par définir celui-ci.
Puis nous mettrons en évidence de manière théorique par les chiffres les avantages de l'utilisation d'une fréquence d'échantillonnage et d'un nombre de bits élevés et nous terminerons par l'examen de quelques mesures comparatives que nous avons réalisées avec des extraits musicaux en qualité CD et ces mêmes extraits dans un échantillonnage supérieur, d'une part sur supports physiques (CD et DVD-Audio), et d'autres part sous forme de fichiers stockés sur un ordinateur.
Qu’est ce que l'échantillonnage ?
L'échantillonnage d’un signal, c’est prendre un certain nombre de mesures de ce signal chaque seconde à intervalles réguliers (qu’il soit audio ou bien vidéo, en fait globalement on peut échantillonner toute tension analogique, quelle qu’en soit l’origine) et coder la valeur analogique de ces échantillons sur un certain nombre de bits.
Ainsi, l'échantillonnage du CD se fait à 44,1 kHz sur 16 bits, ce que tout le monde sait.
La valeur 44,1 kHz représente la fréquence d’échantillonnage, que nous noterons Fe, et la conversion de la valeur échantillonnée sur 16 bits est appelé "quantification".
Pour faciliter la suite de nos explications, nous choisirons la fréquence d'échantillonnage de 176,4 kHz parce que celle-ci est un multiple entier de 44,1 kHz (x 4), mais nous arrondirons ces fréquences à 44 kHz et 176 kHz pour les calculs.
Avec la quantification à 44 kHz sur 16 bits, on va prendre 44 000 échantillons du signal (un tous les 1 /44 000ème de seconde) et coder la valeur de chacun de ces échantillons sur 16 bits.
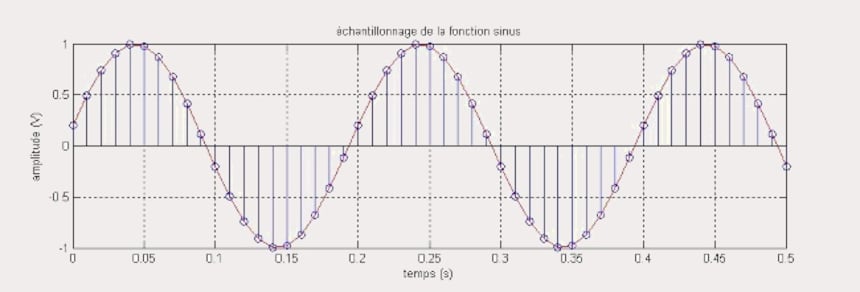
Cependant, le Théorème de Shannon dit que l'on doit choisir une fréquence d'échantillonnage au moins deux fois égale au signal maximum à échantillonner, mais c'est une limite théorique et en pratique on se donne un peu de marge.
Cela revient aussi à dire que l'on ne peut pas coder un signal de fréquence supérieure à la moitié de la fréquence d’échantillonnage, donc une fréquence de 22 kHz avec une Fe de 44 kHz.
Quel est donc l’avantage de choisir une fréquence d’échantillonnage plus élevée ?
Nous venons de voir qu’avec une Fe de 44 kHz on ne peut pas coder des fréquences supérieures à 22 kHz, et on n’obtient alors pour cette dernière que 2 échantillons (44 kHz / 22 kHz), le minimum pour pouvoir reconstruire le signal analogique d’origine, mais c'est quand même peu.
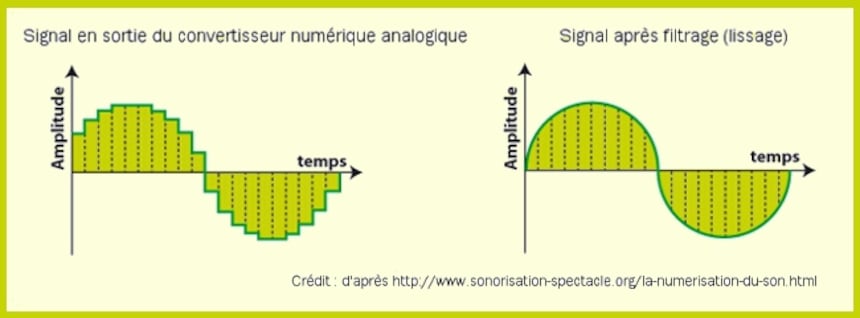
Choisissons maintenant d'échantillonner la fréquence de 11 kHz. Avec cette même Fe de 44 kHz, on obtient 4 échantillons (44 kHz / 11 kHz) pour reconstruire le signal (ce n’est pas énorme mais c’est suffisant) même s’il faudra lisser énergiquement le signal en "marches d’escalier" issu du convertisseur numérique analogique.
Toujours selon le Théorème de Shannon, avec une Fe de 176 kHz on peut coder une fréquence jusqu'à 88 kHz, ce qui est largement au-delà de la perception de l'oreille humaine, mais là encore, on n'obtient que 2 échantillons (176 kHz / 88 kHz).
En revanche, en échantillonnant la fréquence de 11 kHz à 176 kHz, on obtient 16 échantillons (176 kHz / 11 kHz) pour reconstruire le signal.
C'est 4 fois plus qu’avec la Fe de 44 kHz du CD (on reste dans le même rapport que celui des fréquences d’échantillonnage, ce qui est tout à fait logique), et pour une fréquence de 22 kHz on obtient 8 échantillons, ce qui est très bien et largement supérieur aux 2 échantillons obtenus (44 kHz / 22 kHz) avec la Fe de 44 kHz du CD.
L’avantage est loin d’être négligeable en termes de précision et la reconstruction du signal n’en sera que meilleure, donc la fidélité y gagnera.
C'est donc bel et bien sur ce réel avantage "prouvé" qu'il faut insister et non sur la possibilité de pouvoir coder des fréquences inaudibles par un être humain (bien que des débats aient lieu sur ce sujet à propos de l'utilisation "de super tweeter" capables de reproduire les ultrasons et qui amélioreraient le rendu sonore, dans la mesure où la source, bien sûr, contiendrait des signaux supérieurs à 20 kHz).
Il nous faut maintenant aussi tenir compte du fait que l'augmentation de la fréquence d'échantillonnage va généralement de pair avec une augmentation du nombre de bits, ceux-ci passant alors de 16 à 24.
Mais quels sont donc les avantages apportés par l'utilisation d'un nombre de bits plus élevé ?
Comme nous l'avons montré dans cet article, avec 16 bits on peut coder 65 536 valeurs de tensions différentes et obtenir une dynamique (théorique) d'un peu plus de 96 dB.
Avec 24 bits, ces valeurs passent respectivement à 16.777.216 (224) et 144,5 dB (théoriques), des différences qui ne sont pas minces.
Voici un visuel très parlant sur les niveaux sonores exprimés en dB SPL (Sound Pressure Level ou niveau de pression sonore) et leurs valeurs en pression sur un baromètre (puisque le son est une suite de pressions et de dépressions), ainsi que les niveaux maximum que l'on peut coder sur 16 bits et sur 24 bits en prenant comme référence 0 dB le seuil de l'audibilité.
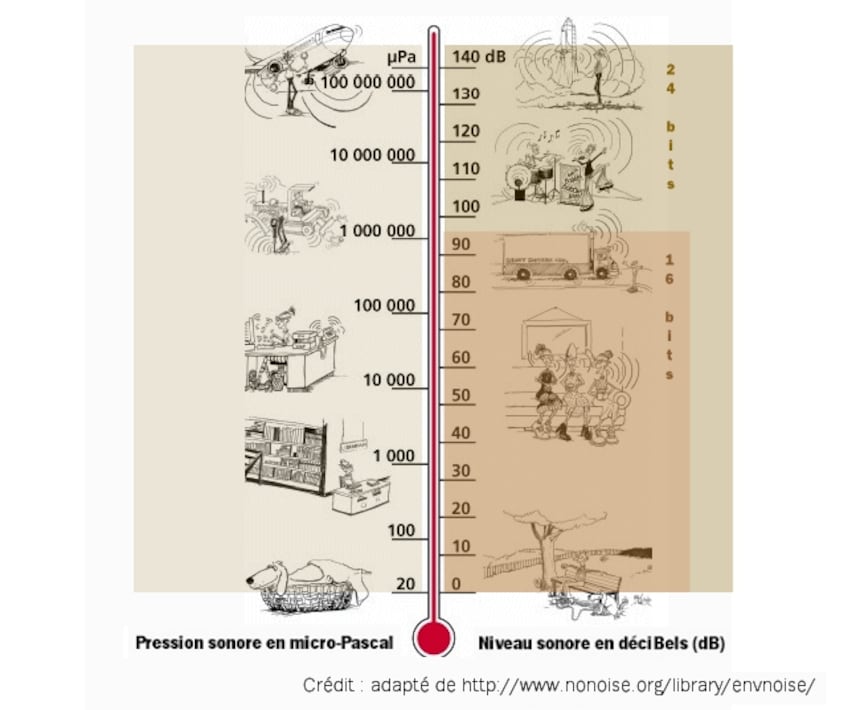
Bien sûr, en pratique on n'utilise pas comme référence le seuil de l'audibilité mais, à l'inverse, le niveau maximum que l'on va avoir à enregistrer afin d'éviter tout phénomène de saturation, comme avec les bons vieux enregistreurs à bande ou à cassette, les niveaux inférieurs se trouvant alors repoussés vers le bas de 96 dB avec 16 bits et de 144 dB avec 24 bits.
On peut déjà déduire de ce fait que pour un même niveau sonore maximum, le codage sur 24 bits permettra d'enregistrer un niveau minimum plus faible de 48 dB (144 - 96), soit environ 250 fois moindre, ce qui permettra une meilleure perception des passages les plus faibles et donc des plus petites variations de dynamique.
Cependant, et ce chiffre trouvé sur cette page Wikipedia m'a un peu étonné (la différence avec le visuel ci avant est de 20 dB), un grand orchestre peut délivrer un niveau sonore de 140 dB, c'est-à-dire qu'on ne peut pas coder toute sa dynamique sur 16 bits (en supposant que les passages faibles soient très faibles, ce qui n'est pas rare, quand ce n'est pas un arrêt net du jeu des musiciens suivi d'un subit fortissimo comme dans certaines symphonies de Mahler) et qu'il faut alors recourir à de la compression de dynamique, alors que les 144 dB de dynamique disponibles avec 24 bits permettent de l'enregistrer sans user de compression.
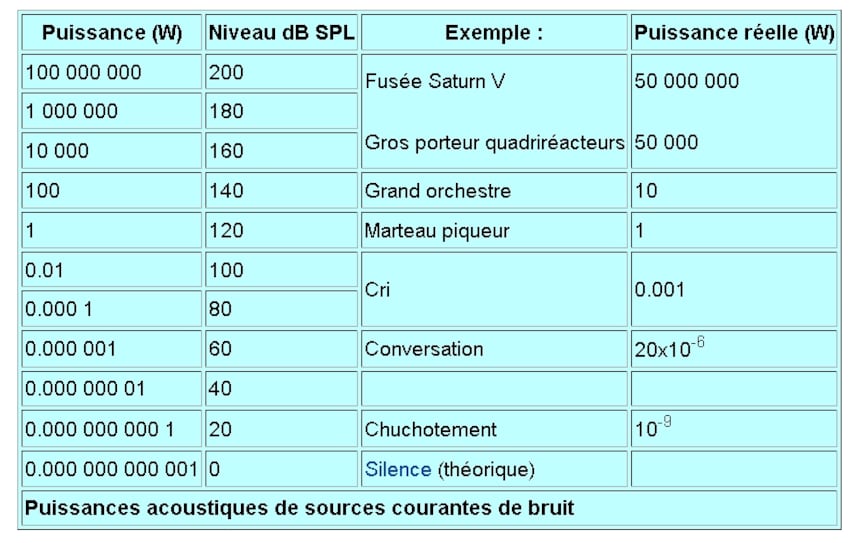
On voit donc que le gain apporté par un codage sur 24 bits par rapport à un codage sur 16 bits permet de gagner à la fois dans les plus faibles niveaux sonores et à la fois dans les plus forts niveaux, et non uniquement dans ces derniers, comme on le croit généralement.
Synthèse et exemples concrets
En conjuguant une fréquence d'échantillonnage élevée avec une quantification sur 24 bits, on gagne à la fois sur la précision de reconstruction des signaux analogiques et à la fois sur la finesse de restitution des plus faibles signaux et des plus faibles nuances de la dynamique tout en pouvant enregistrer ses plus fortes envolées sans avoir recours à la moindre compression.
On peut donc effectivement parler d'audio en haute définition, terme qui n'est pas usurpé, car reposant sur des réalités qui découlent de la technique, ce que l'on vient de prouver, et non sur des arguments commerciaux sans fondement.
Il faut quand même souligner que reproduire une dynamique de 144 dB avec un ensemble domestique de reproduction sonore est très difficilement réalisable, à moins de disposer d'enceintes à très haut rendement capables de délivrer des niveau sonores suffisamment audibles avec de très faibles puissances et supporter les pointes de dynamique sans broncher, et encore.
Je vais maintenant relater l'expérience à laquelle je me suis livré très récemment pour tenter de chiffrer le gain en dynamique du DVD-Audio (codé sur 24 bits à 48 kHz) de la Symphonie Alpestre de Richard Strauss, interprétée par la Staatskapelle de Dresde dirigée par Rudolf Kempe, par rapport à sa version CD, ceci afin de comparer dans un premier temps des enregistrements sur supports physiques (CD et DVD-Audio).

Cette oeuvre d'une grande majesté utilise un orchestre à l'effectif très important, comme le souligne Wikipédia, et comme on le voit sur la photo ci-dessous, extraite du livret du DVD-Audio EMI :
"L'orchestration en est particulièrement riche, même par rapport aux autres œuvres symphoniques de Strauss. Celui-ci emploie plusieurs instruments inhabituels dont une machine à vent dans les percussions, un heckelphone, espèce de hautbois au registre plus grave, ou l'emploi d’aérophones, dispositifs permettant de tenir une note particulièrement prolongée aux vents. Il emploie également, en plus du pupitre des vents de l'orchestre, une fanfare séparée constituée de 12 cors, deux trompettes et deux trombones."

Pour ce, j'ai utilisé un lecteur Panasonic DVD-RA61 pour lire la version DVD-Audio, et un lecteur Sony DVP-NS05V pour lire la version CD. Tous deux étaient reliés à un convertisseur numérique analogique NuForce DAC-9 par cordon optique, afin de bénéficier d'une liaison identique.
Comme je dispose également d'un petit dB-mètre (pas un appareil de compétition, mais suffisant pour procéder à des comparaisons et qui peut mémoriser le niveau maximum ou le niveau minimum), j'ai monté celui-sur un trépied photo afin qu'il ne puisse pas bouger, et je l'ai installé devant ma place d'écoute.
Je tiens à préciser que cet enregistrement de Rudolf Kempe date de 1971 et est donc d'origine analogique et que les enregistreurs à bande de l'époque n'offraient pas les performances "extrêmes" que l'on atteint aujourd'hui en termes de dynamique avec les enregistreurs numériques. J'ai commencé avec la version CD en écoutant les plages 1 et 2 qui sont contiguës, la plage 1 étant assez calme, tandis que la transition avec la plage s'opère avec une "explosion" de dynamique.
La plage 1 m'a permis de relever le niveau de pression sonore minimum et la plage 2 le niveau de pression sonore maximum.
J'ai fait la même opération avec la version DVD-Audio et relevé les résultats.
Voici l'ensemble de ces résultats :
CD :
niveau mini : 53,9 dB
niveau maxi : 79,9 dB
Δ = 26 dB
DVD-Audio :
niveau mini : 53,6 dB
niveau maxi : 81,8 dB
Δ = 28,2 dB
Différence entre le niveau max DVD-Audio et le niveau max CD = 1,9 dB
Les 0,3 dB de différences sur le niveau mini trouvent certainement leur explication dans le fait que le codage sur 24 bits permet une meilleure résolution des micro écarts de dynamique que le codage sur 16 bits, comme nous l'avons vu auparavant, ce qui se traduit dans notre cas par une mesure plus fine du niveau mini avec le DVD-Audio.
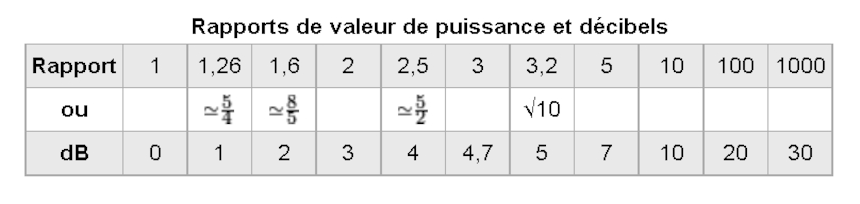
Ces mesures montrent clairement un écart de niveau de 1,9 dB sur les niveaux maxi (1,55 fois plus élevé, soit 101,9 / 10, voir aussi le tableau ci-dessous) en faveur du DVD-Audio codé sur 24 bits à 48 kHz, preuve s’il en est que le terme Studio Masters pour ce genre de fichier n’est pas un argument marketing et qu'un fichier en 24 bits, même à 48 kHz, est techniquement supérieur au fichier en 16 bits à 44 kHz ou au CD, même avec un enregistrement d'origine analogique, dans la mesure où celui-ci est de qualité.
Afin de disposer également d'une comparaison avec un enregistrement numérique récent sous forme dématérialisée, j'ai choisi de comparer les versions en fichiers WAV 16 bits à 44 kHz et WAV 24 bits à 96 kHz de la symphonie N°5 de Mahler par l'Orchestre Symphonique de San Francisco dirigé par Michael Tison Thomas, oeuvre dont l'introduction du premier mouvement comporte une montée progressive vers une très importante pointe de dynamique.

Ces fichiers ont été lus sur un EEE PC avec le logiciel Foobar2000 en mode Kernel Streaming, volume au maximum, et l'ordinateur a été relié en USB au même convertisseur NuForce DAC-9. La lecture de ces deux fichiers s'est donc faite de manière absolument identique, et j'ai procédé aux mêmes mesures que précédemment, mesures que voici :
Fichier WAV 16 bits à 44 kHz :
niveau mini : 48,4 dB
niveau maxi : 83,9 dB
Δ = 35,5 dB
Fichier WAV 24 bits à 96 kHz :
niveau mini : 47,7 dB
niveau maxi : 87,8 dB
Δ = 40,1 dB
Différence entre le niveau maxi en WAV 24 bits à 96 kHz et le niveau maxi en WAV 16 bits à 44 kHz = 3,9 dB
Déjà, on remarque que l'écart de dynamique sur chaque fichier est très important et que la différence entre les niveaux maxi des deux versions est de 3,9 dB.
Cela représente un facteur de 2,45, ce qui est très élevé et prouve l'écrasante supériorité du fichier WAV 24 bits à 96 kHz sur le fichier WAV 16 bits à 44 kHz.
Et là encore on remarque que la mesure du niveau minimum est plus fine de 0,7 dB.
Et avec cette oeuvre, même si les mesures chiffrent l'importance des différences en terme de performance dynamique, l'écoute comparative se révèle de suite tout aussi parlante car la dynamique de la version Studio Masters est véritablement "explosive" !
Qui a dit que les fichiers Studio Masters n'avaient aucun intérêt ?
Liens vers articles en rapport :